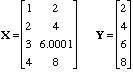Author Archives: Barry M. Wise

Version 6.0 of PLS_Toolbox, Solo and Solo+MIA will be out this fall. There will be lots of new features, but right at the moment I’m having fun playing with one in particular: the Analysis Report Writer (ARW). The ARW makes documenting model development easy. Once you have a model developed, just make the plots you want to make, then select Tools/Report Writer in the Analysis window. From there you can select HTML, or if you are on a Windows PC, MS Word or MS Powerpoint for saving your report. The ARW then writes a document with all the details of your model, along with copies of all the figures you have open.

As an example, I’ve developed a (quick and dirty!) model using the tablet data from the IDRC shootout in 2002. The report shows the model details, including the preprocessing and wavelength selection, along with the plots I had up. This included the calibration curve, cross-validation plot, scores on first two PCs, and regression vector. But it could include any number and type of plots as desired by the user. Statistics on the prediction set are also included.

Look for Version 6.0 on our web site in October, or come visit us at FACSS, booth 48.

BMW

Thanks to everybody that responded to the last post on Accuracy of PLS Algorithms. As I expected, it sparked some nice discussion on the chemometrics listserv (ICS-L)!

As part of this discussion, I got a nice note from Klaas Faber reminding me of the short communication he wrote with Joan Ferré, “On the numerical stability of two widely used PLS algorithms.” [1] The article compares the accuracy of PLS via NIPALS and SIMPLS as measured by the degree to which the scores vectors are orthogonal. It finds that SIMPLS is not as accurate as NIPALS, and suggests adding a re-orthogonalization step to the algorithms.

I added re-orthogonalization to the code for SIMPLS, DSPLS, and Bidiag2 and ran the tests again. The results are shown below. Adding this to Bidiag2 produces the most dramatic effect (compare to figure in previous post), and improvement is seen with SIMPLS as well. Now all of the algorithms stay within ~1 part in 10¹² of each other through all 20 LVs of the example problem. Reconstruction of X from the scores and loadings (or weights, as the case may be!) was improved as well. NIPALS, SIMPLS and DSPLS all reconstruct X to within 3e-16, while Biadiag2 comes in at 6e-13.

The simple fix of re-orthogonalization makes Bidiag2 behave acceptably. I certainly would not use this algorithm without it! Whether to add it to SIMPLS is a little more debatable. We ran some tests on typical regression problems and found that the difference on predictions with and without it was typically around 1 part in 10⁸ for models with the correct number of LVs. In other words, if you round your predictions to 7 significant digits or less, you’d never see the difference!

That said, we ran a few tests to determine the effect on computation time of adding the re-orthogonalization step to SIMPLS. For the most part, the effect was negligible, less than 5% additional computation time for the vast majority of problem sizes and at worst a ~20% increase. Based on this, we plan to include re-orthogonalization in our SIMPLS code in the next major release of PLS_Toolbox and Solo, Version 6.0, which will be out this fall. We’ll put it in the option to turn it off, if desired.

BMW

[1] N.M. Faber and J. Ferré, “On the numerical stability of two widely used PLS algorithms,” J. Chemometrics, 22, pps 101-105, 2008.

In 2009 Martin Andersson published “A comparison of nine PLS1 algorithms” in Journal of Chemometrics[1]. This was a very nice piece of work and of particular interest to me as I have worked on PLS algorithms myself [2,3] and we include two algorithms (NIPALS and SIMPLS) in PLS_Toolbox and Solo. Andersson compared regression vectors calculated via nine algorithms using 16 decimal digits (aka double precision) in MATLAB to “precise” regression vectors calculated using 1000 decimal digits. He found that several algorithms, including the popular Bidiag2 algorithm (developed by Golub and Kahan [4] and adapted to PLS by Manne [5]), deviated substantially from the vectors calculated in high precision. He also found that NIPALS was among the most stable of algorithms, and while somewhat less accurate, SIMPLS was very fast.

Andersson also developed a new PLS algorithm, Direct Scores PLS (DSPLS), which was designed to be accurate and fast. I coded it up, adapted it to multivariate Y, and it is now an option in PLS_Toolbox and Solo. In the process of doing this I repeated some of Andersson’s experiments, and looked at how the regression vectors calculated by NIPALS, SIMPLS, DSPLS and Bidiag2 varied.

The figure below shows the difference between various regression vectors as a function of Latent Variable (LV) number for Melter data set, where X is 300 x 20. The plotted values are the norm of the difference divided by the norm the first regression vector. The lowest line on the plot (green with pluses) is the difference between the NIPALS and DSPLS regression vectors. These are the two methods that are in the best agreement. DSPLS and NIPALS stay within 1 part in 10¹² out through the maximum number of LVs (20).

The next line up on the plot (red line and circles with blue stars) is actually two lines, the difference between SIMPLS and both NIPALS and DSPLS. These lie on top of each other because NIPALS and DSPLS are so similar to each other. SIMPLS stays within one part in 10¹⁰ through 10 LVs (maximum LVs of interest in this data) and degrades to one part in ~10⁷.

The highest line on the plot (pink with stars) is the difference between NIPALS and Bidiag2. Note that by 9 LVs this difference has increased to 1 part in 10⁰, which is to say that the regression vector calculated by Bidiag2 has no resemblance to the regression vector calculated by the other methods!

I programmed my version of Bidiag2 following the development in Bro and Eldén [6]. Perhaps there exist more accurate implementations of Bidiag2, but my results resemble those of Andersson quite closely. You can download my bidiag.m file, along with the code that generates this figure, check_PLS_reg_accuracy.m. This would allow you to reproduce this work in MATLAB with a copy of PLS_Toolbox (a demo would work). I’d be happy to incorporate an improved version of Bidiag in this analysis, so if you have one, send it to me.

BMW

[1] Martin Andersson, “A comparison of nine PLS1 algorithms,” J. Chemometrics, 23(10), pps 518-529, 2009.

[2] B.M. Wise and N.L. Ricker, “Identification of Finite Impulse Response Models with Continuum Regression,” J. Chemometrics, 7(1), pps 1-14, 1993.

[3] S. de Jong, B. M. Wise and N. L. Ricker, “Canonical Partial Least Squares and Continuum Power Regression,” J. Chemometrics, 15(2), pps 85-100, 2001.

[4] G.H. Golub and W. Kahan, “Calculating the singular values and pseudo-inverse of a matrix,” SIAM J. Numer. Anal., 2, pps 205-224, 1965.

[5] R. Manne, “Analysis of two Partial-Least-Squares algorithms for multivariate calibration,” Chemom. Intell. Lab. Syst., 2, pps 187–197, 1987.

[6] R. Bro and L. Eldén, “PLS Works,” J. Chemometrics, 23(1-2), pps 69-71, 2009.

It is probably an understatement to say that here are many methods for cluster analysis. However, most clustering methods don’t work well for large data sets. This is because they require computation of the matrix that defines the distance between all the samples. If you have n samples, then this matrix is n x n. That’s not a problem if n = 100, or even 1000. But in multivariate images, each pixel is a sample. So a 512 x 512 image would have a full distance matrix that is 262,144 x 262,144. This matrix would have 68 billion elements and take 524G of storage space in double precision. Obviously, that would be a problem on most computers!

In MIA_Toolbox and Solo+MIA there is a function, developed by our Jeremy Shaver, which works quite quickly on images (see cluster_img.m). The trick is that it chooses some unique seed points for the clusters by finding the points on the outside of the data set (see distslct_img.m), and then just projects the remaining data onto those points (normalized to unit length) to determine the distances. A robustness check is performed to eliminate outlier seed points that result in very small clusters. Seed points can then be replaced with the mean of the groups, and the process repeated. This generally converges quite quickly to a result very similar to knn clustering, which could not be done in a reasonable amount of time for large images.

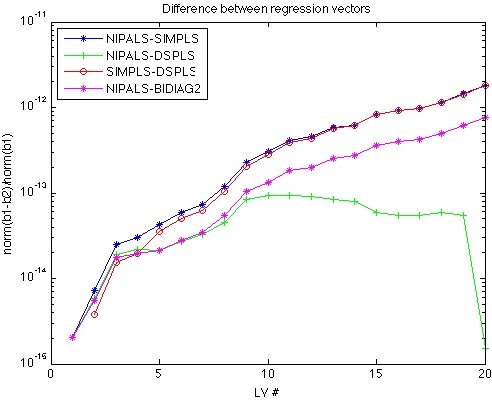
As an example, I’ve used the clustering function on a Landsat image of the Mississippi River. This 512 x 512 image has 7 channels. Working from the purely point-and-click Analysis interface on my 4 year old MacBook Pro laptop, this image can be clustered into 3 groups in 6.8 seconds. The result is shown at the far left. Clustering into 6 groups takes just a bit longer, 13.8 seconds. Results for the 6 cluster analysis are shown at the immediate left. This is actually a pretty good rendering of the different surface types in the image.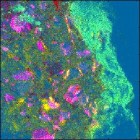

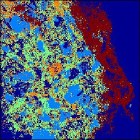As another example, I’ve used the image clustering function on the SIMS image of a drug bead. This image is 256 x 256 and has 93 channels. For reference, the (contrast enhanced) PCA score image is shown at the far left. The drug bead coating is the bright green strip to the right of the image, while the active ingredient is hot pink. The same data clustered into 5 groups is shown to the immediate right. Computation time was 14.7 seconds. The same features are visible in the cluster image as the PCA, although the colors are swapped: the coating is dark brown and the active is bright blue.

Thanks, Jeremy!

BMW

Unscrambler X is out, and CAMO is touting the fact that it is 64-bit. We say, “Welcome to the party!” MATLAB has had 64-bit versions out since April, 2006. That means that users of our PLS_Toolbox and MIA_Toolbox software have enjoyed the ability to work with data sets larger than 2Gb for over 4 years now. Our stand-alone packages, Solo and Solo+MIA have been 64-bit since June, 2009.

And how much is Unscrambler X? They don’t post their prices like we do. So go ahead and get a quote on Unscrambler, and then compare. We think you’ll find our chemometric software solutions to be a much better value!

BMW